Total Volatile Hydrocarbon Contamination in Compressed Breathing Air

While many compressed air users are aware of the risks that contaminants like Carbon Dioxide (CO2) and Carbon Monoxide (CO) can pose to their breathing air, some may not know the risks of a lesser known contaminant: volatile hydrocarbons. This blog will define “total volatile hydrocarbons”, explain why they are a cause for concern, discuss possible sources for contamination, assist in troubleshooting your system, and give options on how to prevent future contamination. Many of the same tips that can keep your compressor clear of other contaminants can also help prevent failures for total volatile hydrocarbons (TVHC).

A hydrocarbon is defined as “an organic compound consisting only of carbon and hydrogen.” (“Hydrocarbon,” Merriam-Webster) Ethanol, butane and toluene are examples of hydrocarbons. Volatility refers to the tendency of these hydrocarbons to become gases. A substance’s volatility is measured by the rate at which a liquid vaporizes (or transitions) from a liquid to a gas phase. If the liquid has a high vapor pressure, the liquid changes to a gas at a lower temperature and has a high rate of evaporation: volatile (“Volatility of a Liquid,” Duke University). Many specifications refer to THC (Total Hydrocarbons), which is the same as TVHC (Total Volatile Hydrocarbons). Both represent the gaseous or vaporous oil found in compressed air.

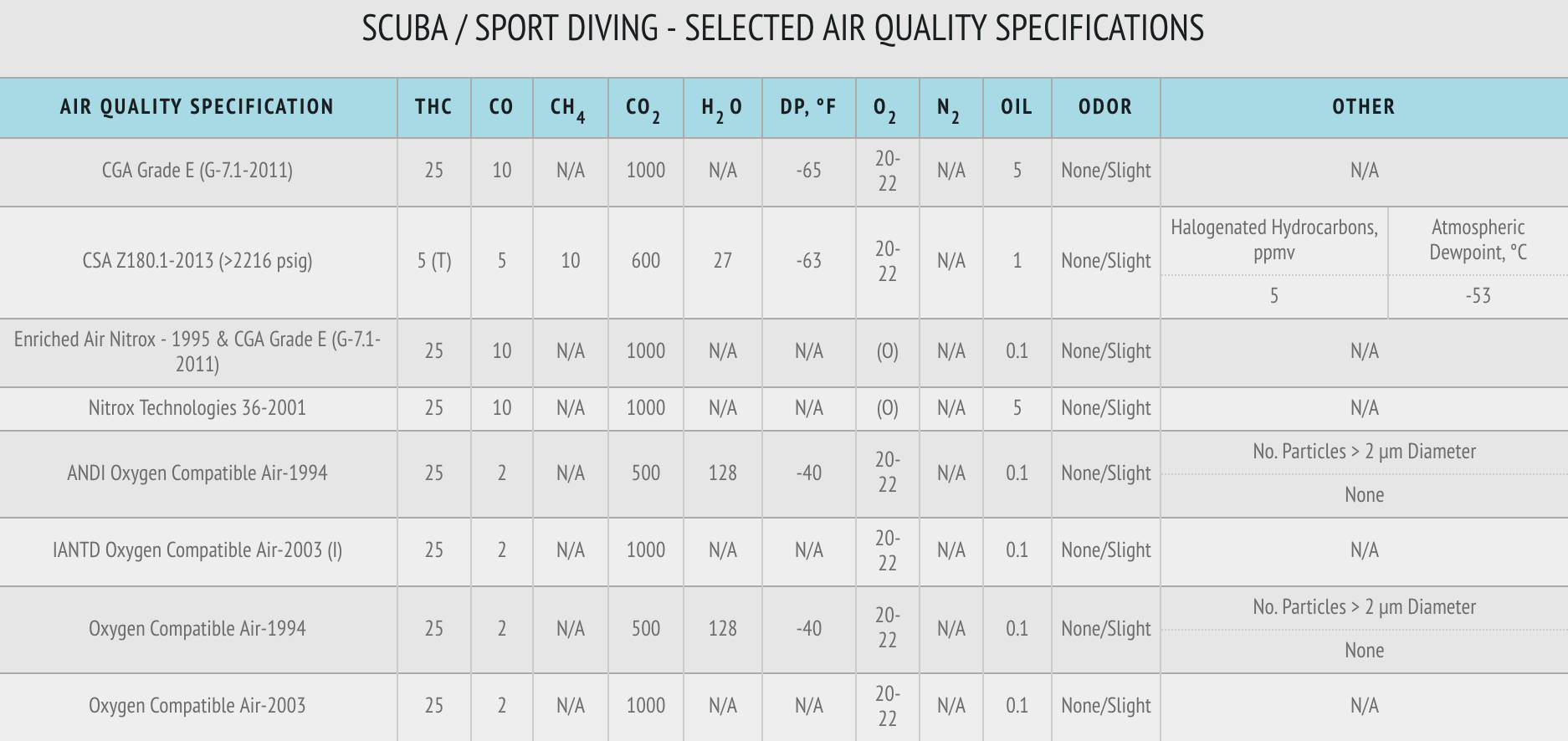
Many hydrocarbons are harmful if inhaled. Toluene, for example, a common solvent with many different applications, can lead to headaches, dizziness and confusion (“OSH Answers Fact Sheet.” Canada, Centre for Occupational Health and Safety). Because of this risk, many specifications set limits for the amount of total hydrocarbons allowable in compressed breathing air. These specifications can vary widely. NFPA 1989, a common breathing air specification among fire departments, sets a limit of 25 parts per million (ppm) for total hydrocarbons, whereas some Canadian Standards Association (CSA) specs set the limit much lower, at 5 ppm.

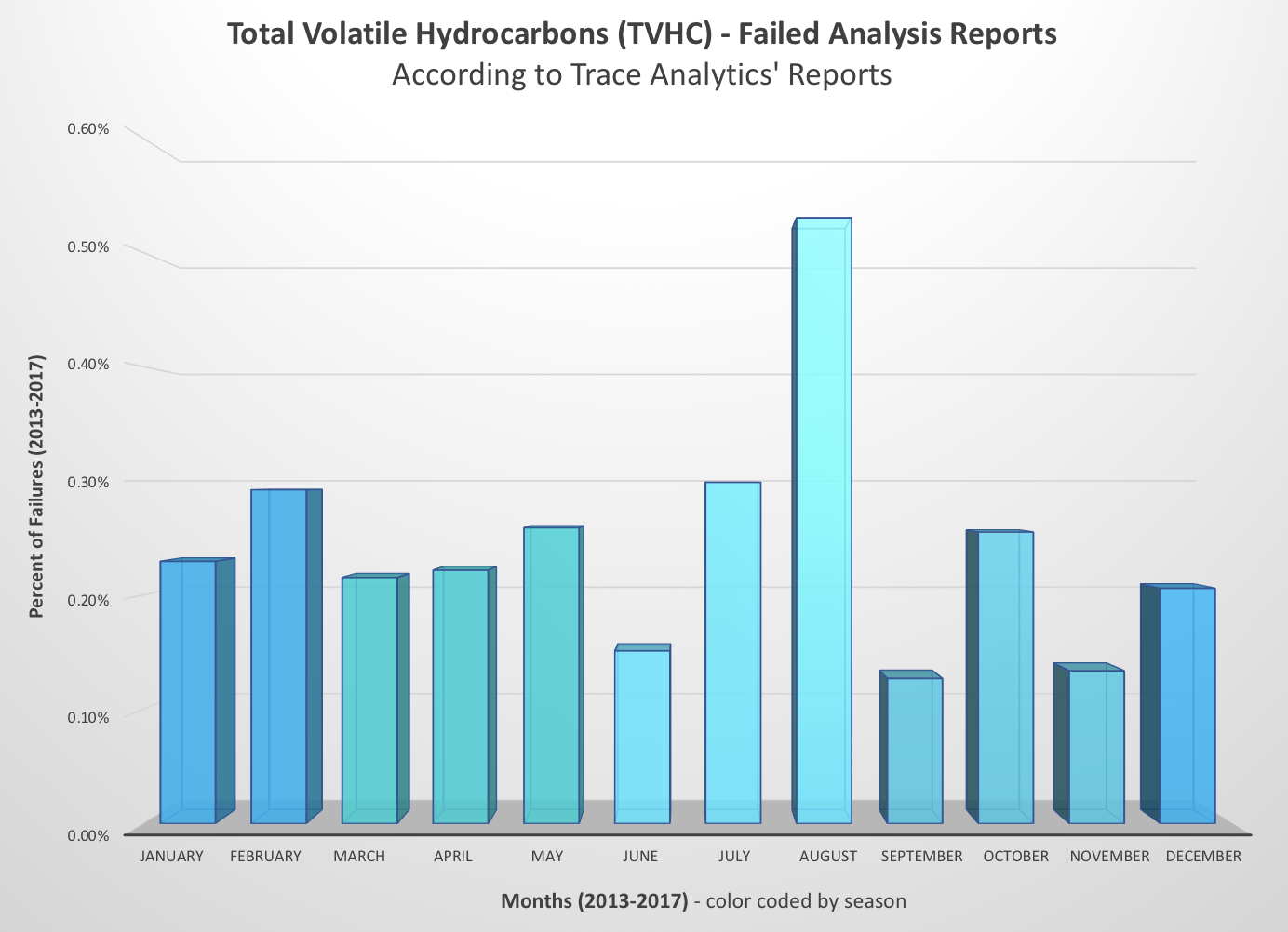
Like CO and CO2, volatile hydrocarbons can enter compressed breathing air both from your intake and from the compressor itself. Many compressors have oil-based lubricants, which can begin to run hot if the compressor is not properly maintained. When this happens, the hydrocarbons in these lubricants burn and are released as gas that can slip by piston rings and enter your air. Trace Analytics’ analyses show more TVHC failures during August, the hottest time of the year. Because of this, a failure for total volatile hydrocarbons can often be a sign that your compressor may need more maintenance checks during the summer months. It can also mean your compressed air is at risk for CO or CO2 contamination.

If your compressor is not the source of your hydrocarbon contamination, then you can inspect your ambient air for answers. The compressor intake pulls air from the environment (ambient air) into your compressor, including the vapors from nearby cleaning establishments, chemical plants, manufacturing plants, or even motor exhaust from idling or passing vehicles. Because your compressor’s filters are not designed to remove hydrocarbons, contaminants present in your ambient air may end up in your compressed breathing air. There are as many sources for hydrocarbon contamination in the environment as there are varieties and uses for hydrocarbons. Dry cleaning facilities and beauty salons, for example, may give off vapors that can lead to contaminated breathing air. Other possible sources of environmental contamination include cleaning supplies, septic tanks, natural gas heaters, poor drainage and decomposition near the intake. If any TVHC source is located near your intake, it can enter your compressed breathing air.

Trace Analytics has the ability, when requested, to identify and quantify these hydrocarbons. Since different hydrocarbons often have different uses, this can be an enormous help in identifying the source of your contamination. Once the source is identified you can move your intake away from the contamination, or, if not possible, take steps to improve the ventilation near your intake.

There is a common theme throughout our breathing air contamination blogs: be aware of how your compressor is functioning. This means keeping up with maintenance as specified by your compressor manufacturer and making sure the air that goes into your compressor is clean. Ensure that your filters and your filter replacement schedule are up to standard for any season or environment. If you’re still not sure what is causing your TVHC failures, contact a compressed air testing expert, and we’ll help troubleshoot your problem.

References:

Canada, Centre for Occupational Health and Safety. “OSH Answers Fact Sheet.” OSH Answers Fact Sheet, 3 Jan. 2017. www.ccohs.ca/oshanswers/chemicals/chem_profiles/toluene.html.

“Hydrocarbon.” Merriam-Webster, 3 May 2018, www.merriam-webster.com/dictionary/hydrocarbon.

“Volatility of a Liquid.” The Alcohol Pharmacology Education Partnership, Duke University, sites.duke.edu/apep/module-4-alcohol-and-the-breathalyzer-test/biology-and-chemistry-connections/volatility-of-a-liquid/.